Der Schiefspiegler nach Anton Kutter, ein obstruktionsloses Spiegelteleskop höchster Abbildungsleistung
Meine nachstehende Abhandlung über den Schiefspiegler beruht im wesentlichen auf Anton Kutters Buch “Der Schiefspiegler, ein Spiegelteleskop für hohe Bilddefinition” als auch auf Mitschriften seiner zu Lebzeiten gehaltenen Vorträge bzw. auf seinen Artikeln in astronomischen Fachzeitschriften.
Schiefspiegler sind Spiegelfernrohre mit gegeneinander verkippten Spiegeln, wobei der Strahlengang Z- bzw. X-förmig verläuft. Diese Bauform erlaubt ein Bild ohne Abschattungen durch Fangspiegel und Halterung (unobstruierter Strahlengang), was Bilddefinition und Kontrastleistung im Vergleich zu herkömmlichen Teleskopsystemen signifikant verbessert.
Das Vermeiden der schädlichen Obstruktion erhöht die Auflösung (Detailschärfe) dieser Optik auf die eines Cassegrain-Teleskops mit ca. 30% höherer Öffnung.
Die Kontrastleistung eines Schiefspieglers ist mit der eines apochromatischen Linsenfernrohrs vergleichbar, wobei wegen der Ausnutzung des physikalischen Effekts der Reflexion im Gegensatz zur Refraktion (Lichtbrechung), völlige Achromasie (Farbfehlerfreiheit) gegeben ist.
 |
|---|
| Anton Kutter 13.6.1903 - 1.2.1985 |
Der Schiefspiegler nach Anton Kutter stellt eine Abwandlung des Cassegrainschen Reflektors dar, wobei Kutters optische Konstruktion von einer exzentrisch in die Öffnung des Cassegrains eingebrachten Blende (z.B. wie zur Sonnenbeobachtung verwendet) ausgeht. Aus diesem Z-förmigen Strahlengang als Ausgangspunkt entwickelte er seinen Schiefspiegler.
Durch das Verkippen der Spiegel treten als Fehler Koma, Astigmatismus und Öffnungsfehler auf, die berichtigt werden müssen.
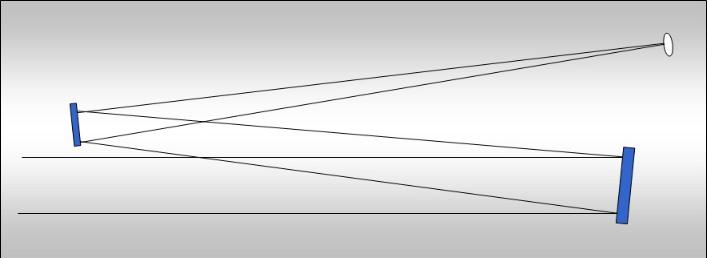 |
|---|
| Strahlengang eines Schiefspieglers nach Kutter |
Ab einer gewissen Größe der Öffnung gehen diese Fehler nicht mehr in der Beugungsbegrenzung unter, so dass eine zusätzliche Keil-Linse in den Strahlengang eingeführt werden muss. Teleskope, bei denen sowohl Spiegel als auch Linsen an der Bildentstehung beteiligt sind, nennt man “katadioptrische Teleskope”.
In seinem Buch “Der Schiefspiegler” beschreibt Kutter die Entwicklung zweier Varianten, bei denen entweder die Koma oder der Astigmatismus minimiert sind.
Kutters genialer Ansatz war, zwei Spiegel gegensätzlicher Krümmung zu verwenden, die zu Bildfehlern mit entgegen gesetztem Vorzeichen führen. Die verbleibende Freiheit, einen geeigneten Reflexionswinkel für den Fangspiegel zu wählen, führt entweder zu astigmatischer bzw. zu Koma-Kompensation.
-
Die anastigmatische Anlage Zwei sphärische Spiegel von relativ langer Brennweite und ein geeigneter Kippwinkel des Fangspiegels ergeben die vollständige Kompensation des Astigmatismus. Die dabei entstehende Koma ist so gering, dass sie im Beugungsscheibchen untergeht (beugungsbegrenzte Optik).
-
Die komafreie Anlage Ein geeigneter Kippwinkel des Fangspiegels führt zu Komafreiheit, aber auch zu einer erheblichen Überkorrektur des Astigmatismus. Eine justierbare Korrekturlinse zwischen Fangspiegel und Brennpunkt kompensiert den erzeugten Astigmatismus.
Durch ein langes Öffnungsverhältnis (typisch ist 1:20 und mehr) werden die Abbildungsfehler beim Schiefspiegler klein gehalten, so dass dieses Spiegelteleskop insbesondere am kontrastarmen Planeten (z.B. Wolkenbänder des Jupiters) hervorragende Abbildungsleistung entwickelt.
Sowohl Hauptspiegel als auch Sekundär-Spiegel sind sphärisch, letzterer konvex. Sphärische Spiegeloptik ergibt beim Polieren die geringste Oberflächenrauhigkeit, weil eine sog. “lokale Retusche” entfällt.
Der Erfinder dieses Spiegelteleskops hatte sich zu Anfang seiner Entwicklung sehr ausführlich mit den Schriften zum Thema “Refractor versus Reflector” auseinandergesetzt, sowie mit Herschels Front View Telescope, mit dem Brachyt von Forster und Fritsch, mit Bernhard Schmidts Horizontalspiegel F/106 und mit den Untersuchungen an Fangspiegelstreben eines Professor Couder.
Nachstehende Auszüge aus Anton Kutters Vortrag, “Mein Weg zum Schiefspiegler”, herausgegeben durch die Schweizerische Astronomische Gesellschaft, “Astro Amateur”, Rascher Verlag, Zürich and Stuttgart, sollen die Zusammenhänge um den Effekt der definitionsvermindernden Silhouettierung vermitteln, indem zunächst die Beugungsfigur eines gegebenen Objektiv-Durchmessers ohne Störung durch Fangspiegel und seine Haltestreben betrachtet wird:
Das “theoretische Auflösungsvermögen” (nach Kutter: “theor. Definition”) ergibt sich aus dem radius “ro” vom Zentrum des ungestörten Beugungsscheibchens zur Mitte des ersten dunklen Rings: ro = 138 Bogensekunden / Objektiv-Durchmesser in Millimeter.
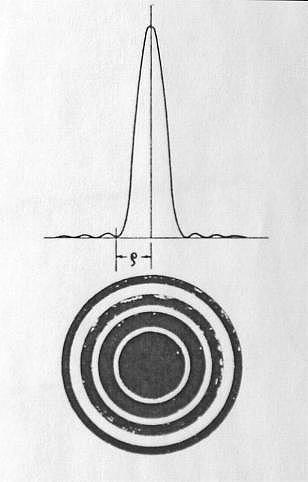 |
|---|
| Abbildung 1 |
Abbildung 1 zeigt, dass der Löwenanteil des zum Beugungsbild formierten Sternenlichts aus punktförmiger Lichtquelle im zentralen, ungestörten Beugungsscheibchen liegt, demgegenüber die Intensitäten des zweiten und dritten Rings relativ gering sind.
Im Sinne maximal erzielbarer Auflösung sind wir als astronomischer Beobachter einer punktförmigen Lichtquelle nur an dem zentralen Scheibchen interessiert, weil nur dieses das kleinste Abbild des Sterns liefert. In ihm sammeln sich 83.9 % des einfallenden Lichts, 16,1% der Energie verteilen sich auf die äußeren Ringe, die man als kontrastmindernden Verlust ansehen muß. Das Verhältnis zwischen Gewinn- und Verlustsaldo wird als der Kontrast-Faktor bezeichnet, der im Idealfall 83,9 zu 16,1 , damit 5,2 beträgt.
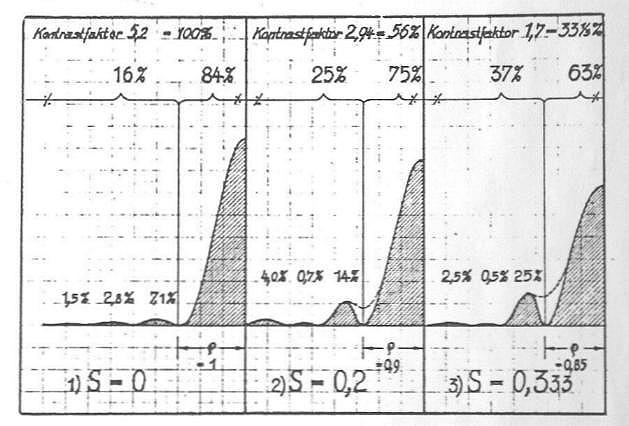 |
|---|
| Abbildung 2 |
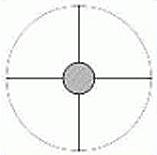
Abbildung 2: Im Verlauf des genannten Artikels wird auf die Untersuchungen der Störung von Fangspiegel und seinen Streben eingegangen. Mittels Abbildung 2 erläutert Kutter am Beispiel eines 150 mm Newton-Spiegels des Öffnungsverhältnis F/8 und mit der kleinen Fangspiegelachse 30 mm, dass aufgrund dieser 20%-Abschattung das Kontrastverhältnis auf den Wert 3,2 absinkt (ohne Berücksichtigung der Streben, also mit planparalleler Glasplatte im Strahlengang, die den Fangspiegel hält).
Bei einem Cassegrain (oder Maksutov) werden die Verhältnisse noch kritischer: Bei typisch 33% Abschattung durch den Gegenspiegel geht der Kontrast-Faktor auf 1,9 zurück, bei Verwendung einer vierarmigen Fangspiegelstrebe sogar auf den Wert 1,7, d.h. auf ca. ein Drittel des Idealwerts.
Wie man erkennt, verlagert sich der Lichtanteil des zentralen Beugungsscheibchens mit fortschreitender Abschattung immer mehr in die umgebenden Beugungsringe (Kutter nennt das “verlorenes Licht”), und im Falle des Cassegrain ist die Helligkeit des ersten Beugungsrings soweit angeschwollen, dass ein auf den vollen Durchmesser des ersten Beugungsrings vergrösserter Bildpunkt vorgetäuscht wird.
Dies stimmt mit den Erfahrungen vieler Kritiker des obstruierten Spiegelteleskops überein: Dass man nämlich, um dieselbe Definition zu erhalten, wie an einem Refraktor, dem Spiegelteleskop eine ca. 30% grössere Öffnung geben müsse.
#Hohe Bilddefinition - Kutters Buchtitel physikalisch erklärt#
Im Folgenden soll die Überlegenheit des unobstruierten Spiegelteleskops verdeutlicht werden, dessen Bildschärfe und Kontrastverhalten denen eines Refraktors ebenbürtig sind.
Die in diesem Artikel angesprochenen optisch-physikalischen Zusammenhänge werden möglichst einfach dargestellt, Mathematik wird gänzlich weggelassen. Damit hat auch der aufgeschlossene Neuling Gelegenheit, sein Optikwissen auf dem Gebiet der Amateurastronomie zu vertiefen.
 |
|---|
| Anton Kutter, Der Schiefspiegler, 1953 |
Kutters oft verwendeter Begriff “hohe Bilddefinition” beinhaltet im Wesentlichen:
-
Detailwiedergabe bzw. Trennvermögen, physikalisch “Auflösung” genannt
-
beste Kontrastwiedergabe
-
völlige Farbfehlerfreiheit
Die ersten beiden Qualitäten beruhen ausschliesslich auf dem abschattungsfreien Strahlengang des Schiefspieglers wie auch der Refraktoren, während das dritte Qualitätsmerkmal ausschliesslich dem physikalischen Effekt der Reflexion vorbehalten bleibt. Bei Linsenteleskopen hingegen ist hoher, kostenintensiver Aufwand zu betreiben, um den physikalisch unabwendbaren Farbfehler, der der Lichtbrechung innewohnt, in ausreichendem Maß zu beheben.
Die Überlegenheit des Refraktors gegenüber dem Spiegelteleskop ist besonders auf dem Gebiet kleinerer Öffnungen offensichtlich, und wird daher insbesonders von Hobby-Astronomen leidenschaftlich diskutiert.
In der Literatur findet man oft nur die allzu summarische Begründung zur Unterlegenheit des Spiegelteleskops, es würde aufgrund seines offenen Tubus empfindlicher auf Luftunruhe reagieren. Des weiteren wird ins Feld geführt, die Genauigkeitsanforderung an eine Spiegelfläche sei viermal höher als an die vier brechenden Flächen eines zweigliedrigen Achromats.
Diese Argumente sind aber nicht die wirkliche Ursache, vielmehr ist es ein grundsätzlicher Unterschied, der zwischen den Strahlengängen der beiden Instrumententypen besteht: Während im Refraktor die vom Stern kommenden Lichtstrahlen in der vollen Ausdehnung der Objektivfläche zum teleskopischen Bild formiert werden, werden sie im obstruierten Spiegelteleskop durch die unvermeidliche Fangspiegelfläche zentral ausgeblendet. Dies soll nachfolgend näher ausgeführt werden.
Ein mathematischer Lichtpunkt, wie dies ein Fixstern ist, wird von einem Objektiv nicht als unendlich kleiner Bildpunkt dargestellt, sondern als endlich große Scheibe, die von einer Reihe verschieden heller Lichtringe umgeben ist. Die Strahlen des vom Stern kommenden Lichtbüschels werden am Rand des Objektivs gebeugt und zu einer Beugungsfigur auseinandergezogen.
Vom Standpunkt der geometrischen Optik aus bedeutet dies nur einen geringfügigen Lichtverlust, der auf die Qualität des Bilds keinen wirklichen Einfluss hat. Vom Standpunkt der Wellen-Optik aus beurteilt, hat diese Abschattung aber eine schwerwiegende Bedeutung, denn genau diese Beugungsfigur ist der kleinste Lichtpunkt, aus dem sich jegliche astronomische Bildszenerie zusammensetzt. Je kleiner und punktförmiger unsere “Pixel” (picture elements) sind, umso trennschärfer und kontrastreicher wird das dargestellte Abbild!
Generell gilt: der Radius der zentralen Scheibe (auch Airy-Scheibchen genannt) beruht auf der Wellennatur eines vibrierenden Lichtquants und hängt nur von der Apertur des Objektivs und der Wellenlänge der Lichtstrahlen ab. Da es für die Lichtbeugung kein Gegenmittel gibt, müssen wir uns damit abfinden.
Neben der absoluten Größe des Beugungsscheibchens ist aber auch die Lichtverteilung innerhalb dieses Gebildes wichtig. Im oberen Teil dieses Posts wird erläutert, wie sich das zum Beugungsbild formierte Licht beim idealen Linsen-Objektiv, bzw. bei der fangspiegel-gestörten Spiegeloptik auf die zentrale Beugungsscheibe bzw. auf die umgebenden Ringe verteilt. Man erkennt, wie die punktförmige Bildinformation fatalerweise “aufgebläht”, und wie die nahe Umgebung des zentralen Bildpunkt als Träger der Bildinformation überdies aufgehellt wird, was einen merklichen Kontrastverlust bewirkt.
Die Zusammenhäge sind leider noch etwas komplexer, weil es neben dem Beugungsscheibchen als kleinstmögliche, punktförmige Fokussierung eines parallelen Strahlenbündels in der Brennebene noch das sog. Spot-Diagramm gibt, welches uns sagt, wie gut (manchmal eher schlecht!) die Strahlfokussierung in Abhängigkeit vom Abstand zur optischen Achse gelingt.
Zum Glück haben wir die freie Wahl der optischen Konstruktion, wie auch die eines geeigneten Öffnungsverhältnisses in der Hand. Beides hat entscheidenden Einfluss auf die Größe des Beugungsscheibchens für ausser-axiale Lichtstrahlen, draußen im Feld. Nachvollziehbar wird dies mittels einer genialen Computersimulation namens WINSPOT.EXE von David Stewick, eine ins Netz gestellte Freeware, die uns verschiedenste Strahldurchdringungs-Diagramme prüfen lässt.
Tatsächlich ist der weitverbreitete, kurzbrennweitige Newton-Parabolspiegel keineswegs das Non-Plus-Ultra der Astro-Optik. Auch beugungstheoretisch ist seine Abbildung zu beanstanden, weil die verschieden langen Brennstrahlen seiner einzelnen Zonen durch Phasenungleichheit das Beugungsbild ungünstig beeinflussen. Jeder Beobachter erkennt dies an der eng begrenzten Vergrösserungsfähigkeit der Bilder eines kurzbrennweitigen Parabolspiegels.
Betrachten wir dazu das Spotdiagramm eines keinesfalls extrem schnellen F/5-Newton-Teleskops und demgegenüber das eines Schiefspieglers in anastigmatischer Anlage, F/28.
Wir vergleichen also folgende Teleskope:
-
Newton-Parabolspiegel mit einer abbildenden Fläche der Öffnung = 150 mm, F = 750 mm und vorgegebenem Gesichtsfeld des Halbwinkels 0,75 Grad (dreimal Vollmond-Durchmesser)
-
Kutter-Teleskop mit zwei abbildenden Flächen der Öffnung = 150 mm, F = 4200 mm und vorgegebenem Feld 0,25 Grad (einfacher Vollmond-Durchmesser)
Der Radius eines Beugungsscheibchens, z.B. im grünen Licht (ca. 500 nm) errechnet sich nach folgender Faustformel: r = 1,22 * Lambda * Brennweite / Öffnung
Konkrete Zahlen eingesetzt, ergibt: r (Newton) = 1,22 * 0,0005 mm * 750 mm / 150 mm = 0,003 mm (Durchmesser 0,006 mm) r (Kutter) = 1,22 * 0,0005 mm * 4200 mm / 150 mm = 0,017 mm (Durchmesser 0,034 mm)
Das Beugungsscheibchen des Kutters ist also fünf- bis sechsmal grösser als beim Newton, letzterer ist also in puncto Trennschärfe überlegen, allerdings ausschließlich auf der optischen Achse.
Sehen wir uns die Spot-Diagramme beider Systeme an. Beim Newton haben wir eine vorzügliche Strahlfokussierung auf der Achse, die theoretisch viel kleiner wäre, als sein Beugungsscheibchen (dargestellt als schwarzer Ring). Doch leidet der F/5-Newton am Feldrand, also schon bei 0,75 Grad Winkeldistanz zur Bildmitte (nach nur 1,5 * Vollmond-Durchmessern) an massiver Koma, dort ist die Strahlfokussierung auf ein monströses Gebilde angewachsen!
Wenn wir uns klarmachen, dass sich die Bildpunkte am Feldrand unseres Newtons aus diesen “Blobs” zusammensetzen, ist klar, dass eine photografische Nutzung des Newtonspiegels unbedingt einen Koma-Korrektor erfordert!
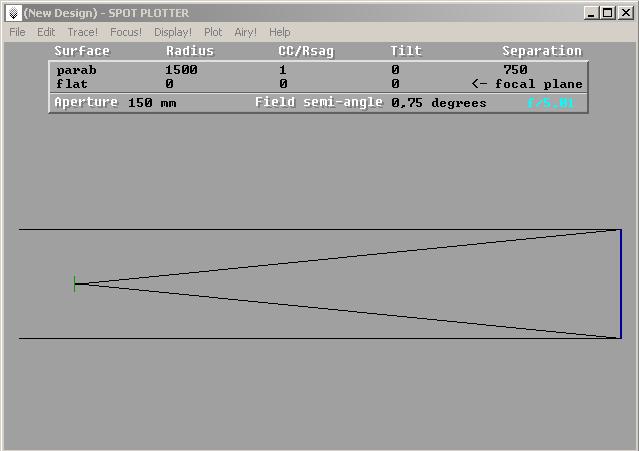 |
|---|
| Newton-Strahlengang |
 |
|---|
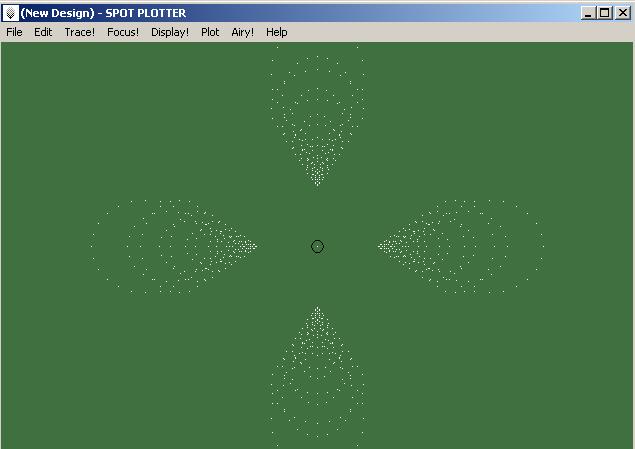
| Newton-Spotplot |
Ganz anders der Kutter: an seinem Feldrand ist der Spot (Strahldurchdringung in der Brennebene) kaum größer als in der Bildmitte. Wir erhalten also ein fast beugungsbegrenztes Feld mit randschärfster Abbildung. Nichts spricht dagegen, großflächige Bildsensoren, z.B. guter Digitalkameras in der Brennebene zu montieren, um formatfüllend z.B. hochauflösende Mondfotos zu bekommen!
 |
|---|
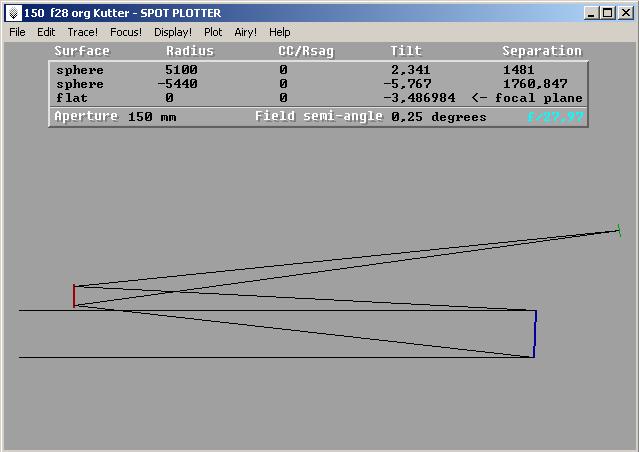
| Kutter-Strahlengang |
 |
|---|
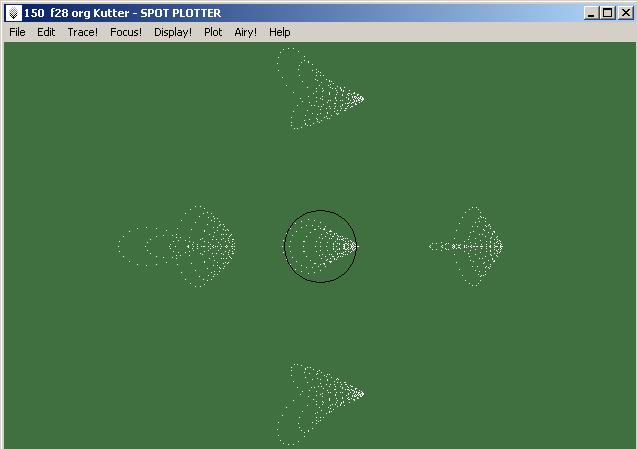
| Kutter-Spotplot |
Wer sich das Programm “WINSPOT” herunterlädt, kann selbst die folgenden, interessanten Erkenntnisse verifizieren:
-
der 150/750-Newton aus obigen Beispiel hat bei einem Feld von ca. 1,5 * Vollmond am Feldrand bereits einen ähnlich großen Spot wie der Schiefspiegler (aber nicht dessen unübertroffenes Kontrastverhalten)
-
das beugungsbegrenzte Feld dieses F/5-Newtons (Spot am Rand dieses Felds nicht größer als sein Beugungsscheibchen) beträgt nur 9 Bogen-Minuten, das sind bloß ca. 10 Jupiter-Durchmesser
Doch neben diesem Hauptmerkmal “Auflösung bzw. Trennschärfe” des obstruktionsfreien Kutter-Teleskops gibt es noch weitere, günstige Merkmale in Hinblick auf optische Vollkommenheit. Nehmen wir uns das weitverbreitete Cassegrain-Teleskop vor. Gerade bei diesem scheint die Priorität hin zu bequemer Handhabbarkeit und Baugröße leider besonders stark verschoben zu sein. Dieser Umstand führt zu erheblichen Abstrichen an optischer Perfektion und erscheint technisch völlig unangebracht, was leicht zu zeigen ist. Nehmen wir als Beispiel ein Spiegelteleskop mit 200 mm Öffnung und seiner optischen Vollkommenheit wegen (Kugelspiegel, mit höchster Genauigkeit herstellbar!) mit 4000 mm Brennweite.
Ein Newton wäre wegen seiner großen Baulänge praktisch unmöglich. Daher entwerfen wir einen Cassegrain, bei welchem sich die 4000 mm Brennweite in einem Tubus unterbringen lässt, der nur etwa 900 mm lang zu sein braucht, zunächst ein ansehnlicher Vorteil in Hinblick auf Transportierbarkeit und Aufstellung. Eine solche Anordnung mit der System-Öffnungsverhältnis F/20 ergibt:
-
Hauptspiegel von 1000 mm Brennweite, also Öffnungsverhältnis F/5
-
Fangspiegel von -320 mm Brennweite und ca. 60 mm Öffnung, damit ca. F/5.3
Aber Achtung: die weitere Betrachtung dieses Systems in Hinblick auf die erforderliche Genauigkeit des Cassegrain-Hauptspiegels im Verhältnis zu dem des Newtons ergibt, dass der Cassegrain-Hauptspiegel F/5 eine 64-fach (!) höhere Flächengenauigkeit verlangt, als der gleichgroße Newton-Hauptspiegel F/20.
Auch wenn die Fertigung eines solchen Spiegels in der Serienproduktion gleichbleibend gut gelingt, so bleibt doch die Tatsache bestehen, dass aIle durch Temperatur- und Schwereeffekte erzeugten Deformationen im selben Verhältnis größer ausfaIlen, als bei dem verglichenen Newton, weil dies die hohe Nachvergrößerung des Cassegrain-Fangspiegels bewirkt! Schon Ludwig Schupmann, Erfinder des Schupmann-Medials, war sich dieser Tatsache bewusst und prägte für dieses riskante Konstruktionsprinzip den Begriff: “optischer Umweg”.
Bedenkt man des weiteren, dass der Fangspiegel eines Cassegrains eine Obstruktion von 60 mm zu 200 mm, gleich 0,3 aufweist, was den Kontrast der Beugungsscheibe um fast 60 % vermindert, wird der Anwender unschwer erkennen, dass der kompakte und bequem zu handhabende Cassegrain dem Schiefspiegler völlig unterlegen ist.
Die optisch-konstruktiven Ausbildungsmerkmale des Kutter-Teleskops sind damit klar umrissen:
-
unobstruierter Strahlengang in Hinblick auf minimales Beugungsscheibchen und bestem Kontrast
-
das Öffnungsverhältnis des Hauptspiegels muss klein sein (max. 1:12), um die sphärische Aberration klein zu halten.
-
lange Brennweite ohne großen optischen Umweg, indem die optischen Kräfte des Systems gleichmäßig auf Haupt- und Fangspiegel verteilt werden
-
der konvexe Sekundärspiegel kann den gleichen Radius wie der Hauptspiegel haben (angenehme, schleif-technische Erleichterung), die Petzval-Bedingung ist dann erfüllt, und das Bildfeld ist geebnet
-
die maximale Öffnung des Schiefspieglers sollte unter 400 mm bleiben; eine Übertragung auf große SpiegeIteleskope ist nicht möglich
Damit liegt der Vorteil des Kutter-Teleskops gegenüber einem vergleichbaren Newton- oder Cassegrain im Fortfall der Beugung am Sekundärspiegel und an dessen Haltestreben. Auflösung und Kontrast bewegen sich auf gleichhohem Niveau wie beim apochromatischen Linsen-Teleskop, was sich positiv insbesondere bei Mond- und Planetenbeobachtungen auswirkt.
Aus diesen Gründen sind Schiefspiegler für den puristischen Mond- und Planetenbeobachter seit langem die Teleskope der Wahl, wenn kein “Teuer-APO” leistungsstarker Öffnung zur Disposition steht.
Schließlich möge es der geneigte Leser dem Autor nachsehen, wenn er zum Schluss noch auf ein weitverbreitetes Phänomen hinweist. Ohne weitere Vorrede auf den Punkt gebracht - wer würde sich einen Refraktor mit großen, tiefen Kratzern und einem mittigen, blinden Fleck auf seinem Fraunhofer-Objektiv zulegen? Im Fall des Spiegelteleskops werden solche Fehler wie selbstverständlich in Kauf genommen, und die dann “Spinnenarme” und “Fangspiegel” heißen!
 |
|---|
Dies, obwohl unstreitig ist, dass Spinnenarme bzw. Fangspiegel aus optischer Sicht mit ein- und demselben, physikalisch bedingten Leistungsverlust wie Kratzer einhergehen.
 |
|---|